When Alex/yaxu mentioned “MSG and its excellent compressor” my interest was immediately piqued - I expected I’d be able to look at the source code and I’m always interested to look at compressor designs - I wasn’t disappointed.
Here we’ll look at the design, work out what makes it special, and discuss possible modifications to expand possible use cases.
note
The version I looked at was the one in Alex’s datadirt which is based largely on MSG (I haven’t checked so there could be differences)
Also - I am not an expert - there could/will be errors here, please email if so :)
Not that I believe experts exist, but…
innards
It took me a while to figure out the action of the compressor, what helped was rearranging things a little bit to present it in a way I could understand.
The code in question is:
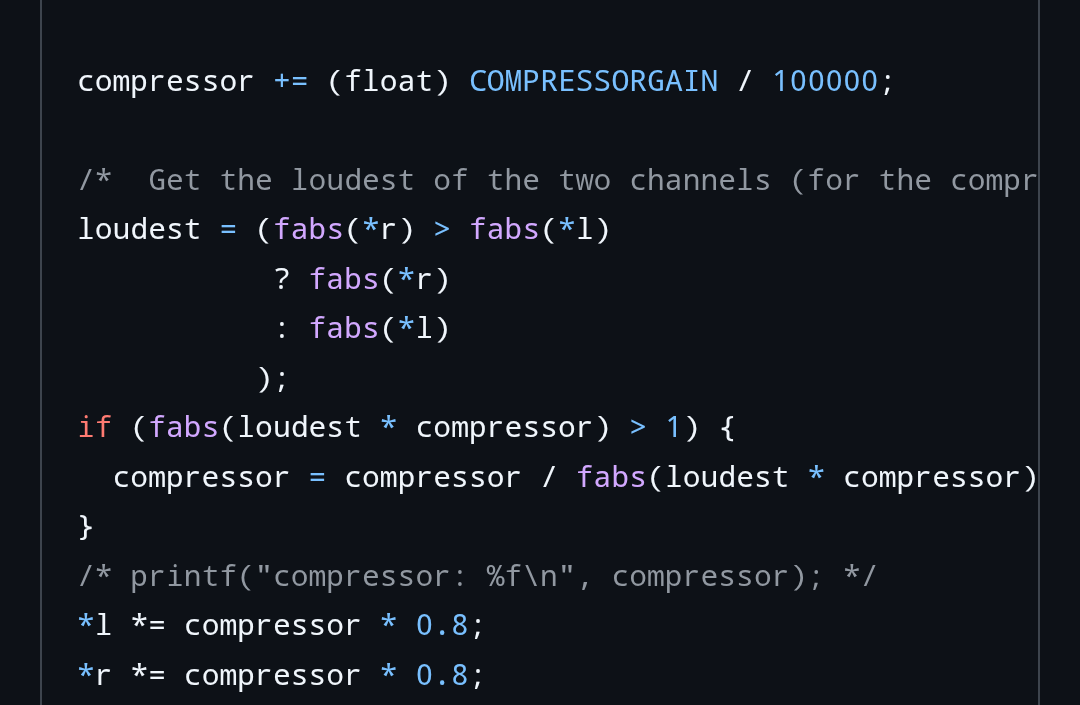
Here we see that it is nice and succinct - always a good sign :)
The COMPRESSORGAIN constant’s value is 200 and controls the speed, or release, of the compressor action. I’m not sure why this wasn’t encoded as 0.002 instead, that’s the value I have used below.
The loudest variable is straighforwardly derived as the comment describes, which is always a good idea to avoid under-controlling loud signals that are panned to either side.
So far so good.
Skipping back to the first line, the incrementing of compressor threw me a bit at first, but it makes sense eventually (took me a while!)
Let’s do some rearranging to simplify things a bit.
First let’s introduce k = 1/compressor for reasons that will become clear.
Then we can also breakdown the abs function next, as abs(x*y) = abs(x)*abs(y) (multiplicativity)
so abs(loudest * compressor) can be rewritten as abs(loudest) * abs(compressor), and seeing as compressor can only be set to a positive value or incremented we can use
loudest * compressor > 1
which is equivalent to
loudest > 1/compressor
then substituting k,
loudest > k
is the if clause.
Now, rearranging the assignment to:
compressor = compressor/compressor * 1/loudest
by taking the same liberties with abs, noticing compressor/compressor = 1 and substituting k again, we obtain:
k = loudest
Putting that all together, and ignoring stereo for now, we get:
k = 1/(1/k + 0.002)
loudest = abs(input)
if loudest > k {
k = loudest
}
output = input / k
output *= 0.8
which is something I can get my head around :)
analysis
The first thing we notice is that the action is peak-hold, that is to say the compression is updated when the input exceeds the previous level of k.
The ratio is infinite, so it’s a limiter. And the gain is updated instantaneously (zero attack) and decays away in an exponential-like way as ~1/t (compressor increases linearly with time and k is 1/compressor).
That might sound fairly conventional, however there some interesting quirks that make it special.
The decay is steeper than exponential at onset, with a ’long tail’.
The gain has no lower bound, so without input k will approach zero and the potential gain will actually increase the input as opposed to attenuate it, a technique known as upward compression. This also means that under limiting conditions, a transient will ‘snap to’ a value of 1, while low end sounds (which are the most prominent in typical music) will be harmonically distorted in proportion to their frequency - the lower the frequency the longer the interval between peaks and the further k will decrease, leading to a bigger jump. All of these things put together make a characterful, punchy and fun effect.
One other thing to note is that until compressor has had a chance to rise (after around half a second) the first transient will need to be greater than ±2 to trigger the limiting action.
so is our analysis correct?
Well, we need to try this out. I could have written some code to feed signals into the design and plot the output values with a library, however that might take a bit of time and also I have a sound engine to hand that can produce recordings which we can view in an application like audacity (I’m still considering alternatives to that for general use but haven’t got round to it yet…)
Let’s put the code in something closer to it’s original form (mono version), shortening variable names:
c += 0.002
l = 1/abs(input)
if l < c {
c = l
}
output = input * c
output *= 0.8
note the comparison has been flipped due to the inversion of l, and that the conditional is equivalent to c = min(c, l).
So:
c += 0.002
c = min(c, 1/abs(input))
input *= c
input *= 0.8
aside: integrating 0.002 at 44100Hz results in a frequency of ~88hz or period ~11ms, so to maintain consistent timing at different sample rates 88/SampleRate could be used instead.
In Syntə, the equivalent code (presented in vertical form) is:
out x
abs
\ 1
min "c
+ 11ms
out "c
mul x
mul 0.8
where " denotes a default value of 0.5 (as in the original compressor) and x is the input value. With one minor difference that, for convenience, "c (which represents the compressor variable) is incremented after the conditional.
If you want to try it you’ll need to define:
[ min, - @, out a, lt 0, mul a, + @, ]
Now let’s run it and see what happens!
screenshots:
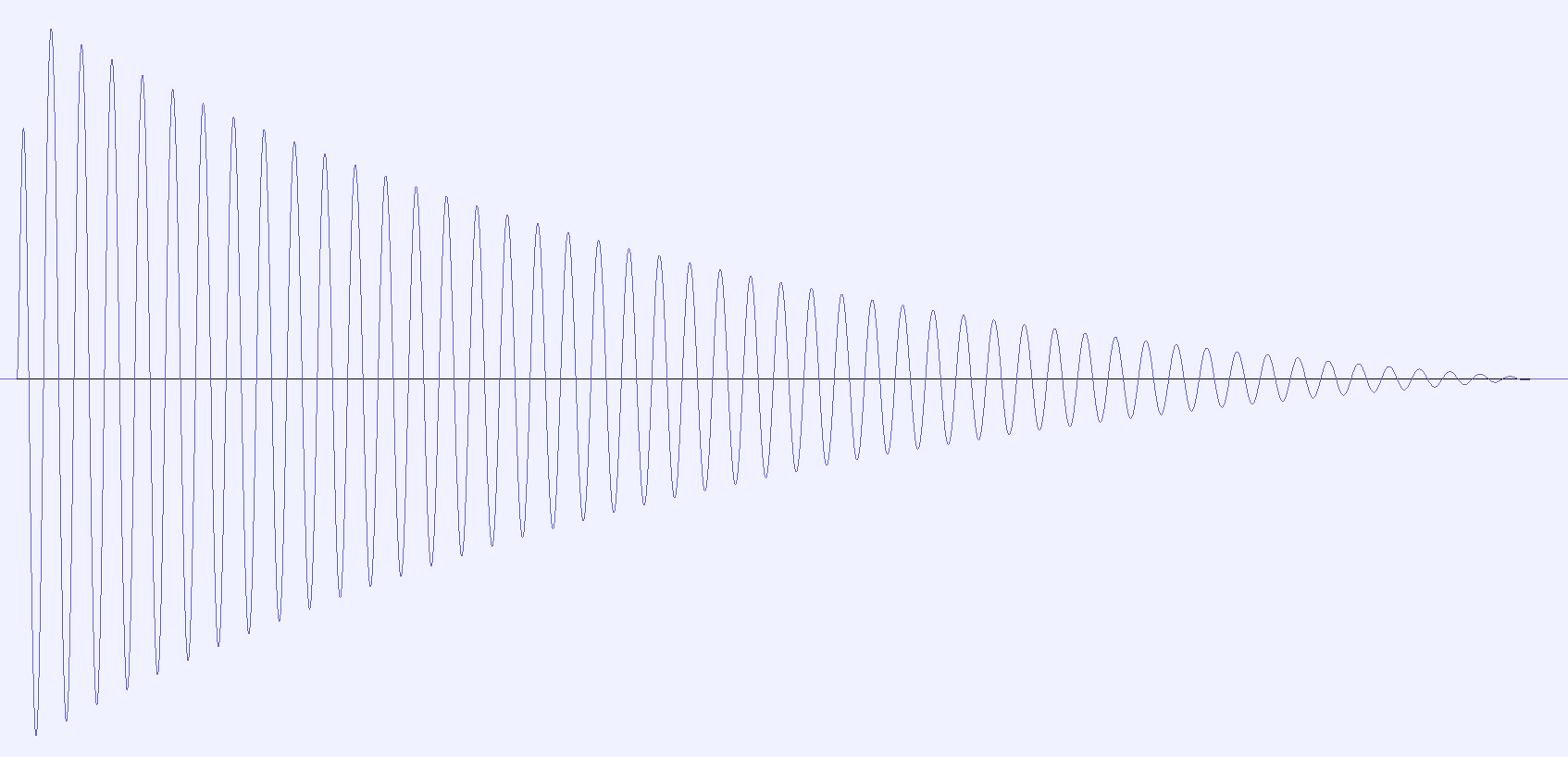
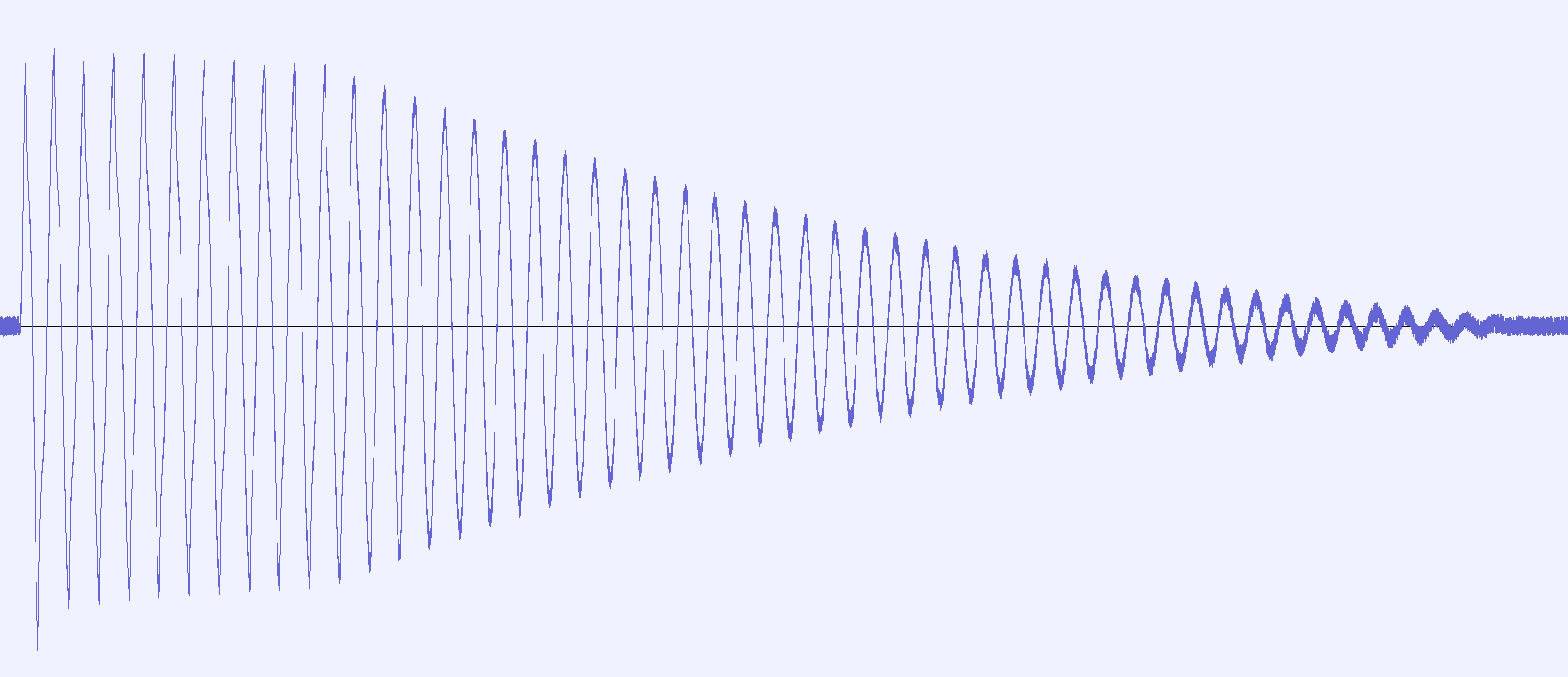
A basic kick drum consisting of a 100Hz sine wave with a slightly rounded exponential decay envelope.
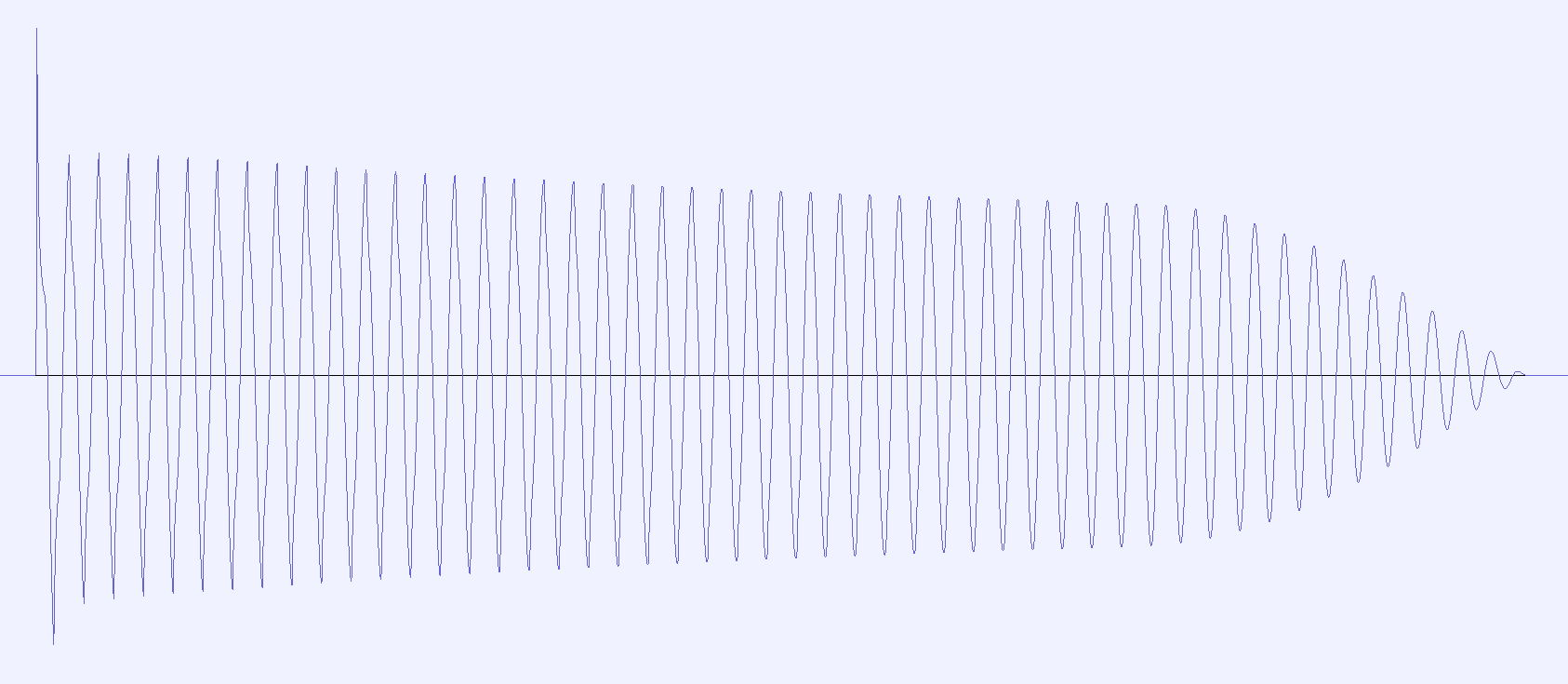
The same kick drum played through the compressor, showing the boost in level.
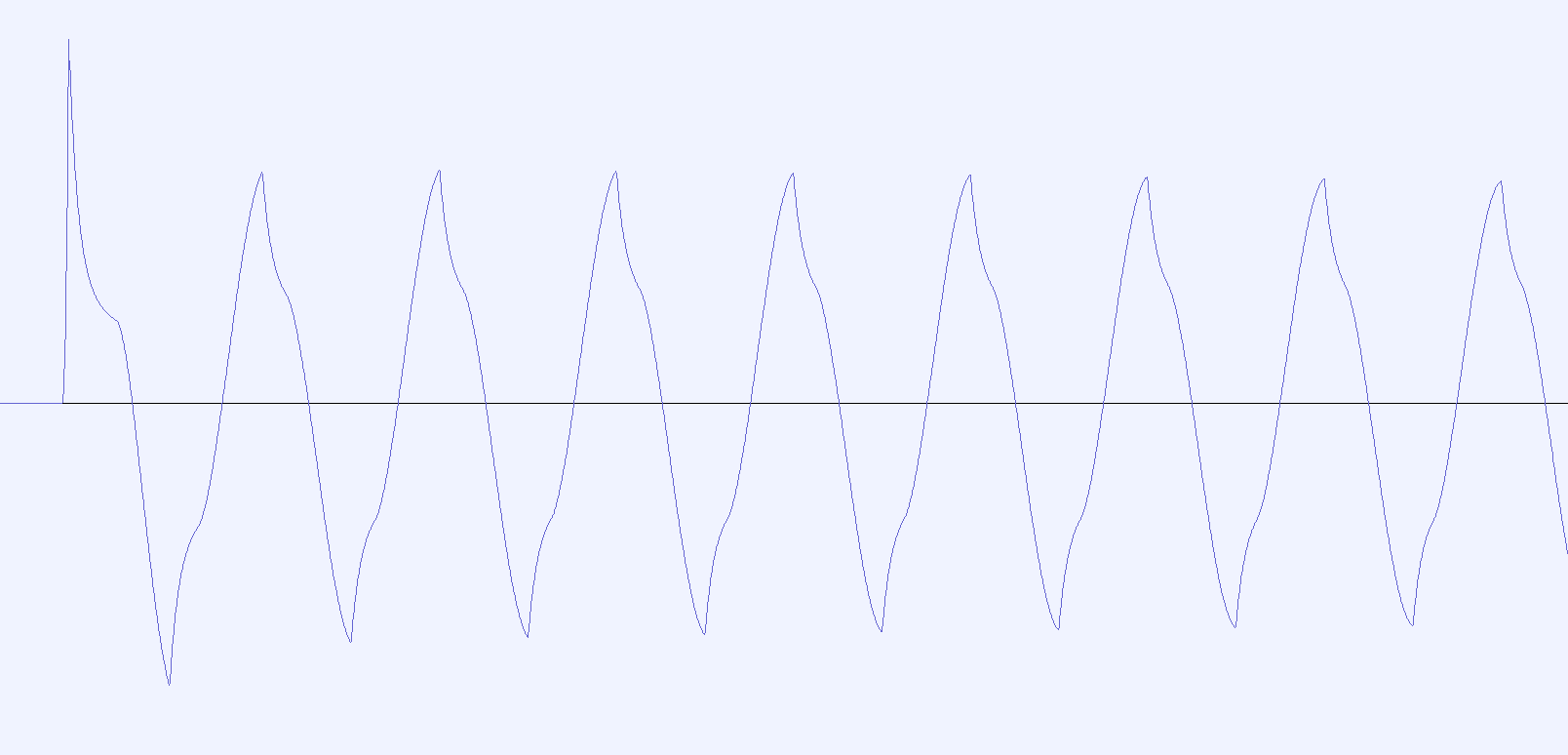
Zoomed in detail of the same waveform showing the harmonic distortion.
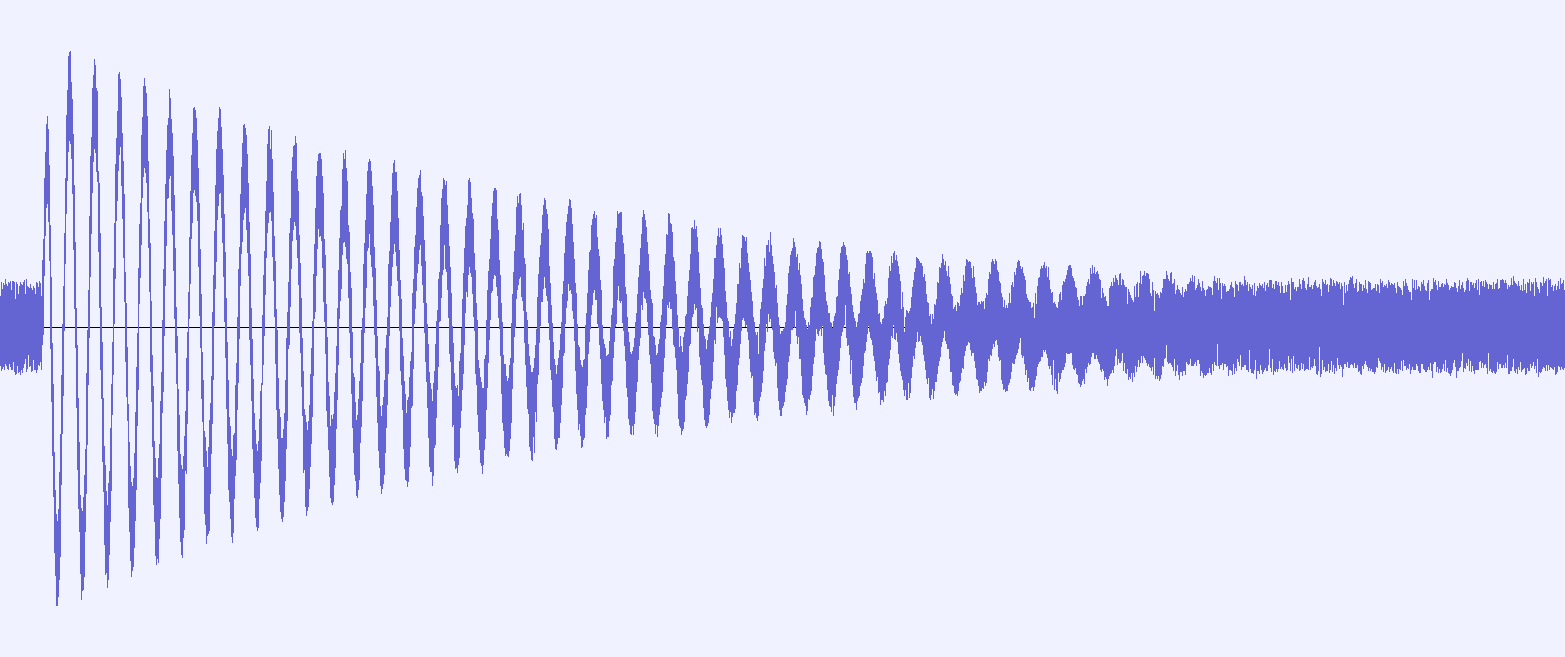
The kick drum with a background of white noise.
Showing the boost in the noise under compression, onset exhibiting ‘pumping’ artefacts.
in practice
Although I haven’t tried the orginal software, I expect this compressor works well for the application it was designed for. Which you could essentially call a bus compressor.
However, if you wanted to use it for other things such as a channel compressor where there might be quiet passages, you could add min 2 before assigning out "c. This will constrain the upward compression to 6db for a milder effect.
Which indeed we see here:
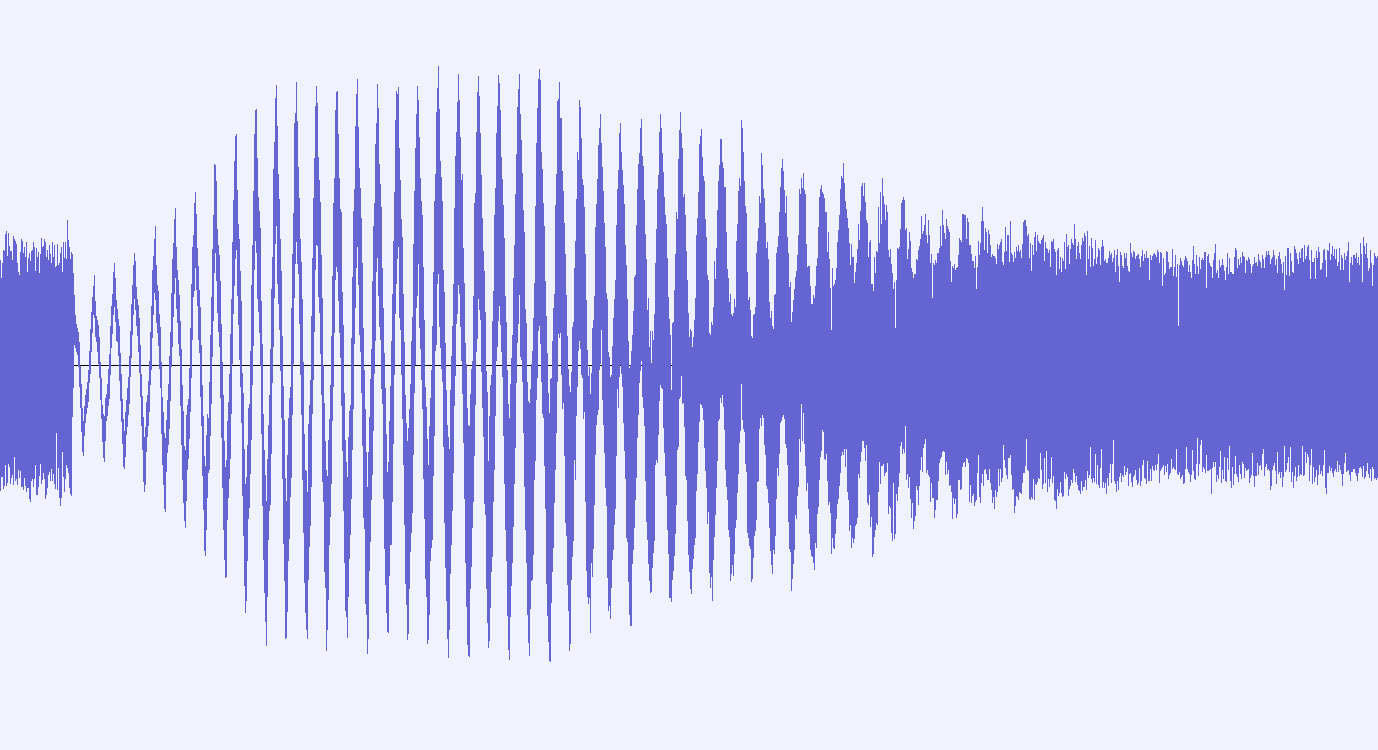
This is a similar input as the previous example, showing a controlled noisefloor. The level of the kick is less ’nailed’ to maximum gain too.
We can run it with 'c (initialised to 1) but this only changes the first onset of limiting.
You could drop the * 0.8 that introduces ~2dB of headroom if you want, given that the zero-attack limiting keeps the output pinned to ±1.
a note of caution: if you are using the original form of this on a loud system, be within reach of a direct level control or have an attentive sound engineer - due to the potentially unconstrained gain at any frequency there is no guarantee you won’t have any painfully loud surprises.
syntax
previously on this blog we have considered code readability and expressiveness. We have another opportunity now to draw a comparison, in this case between Syntə and C. Looking at the examples above, what do we notice? The Syntəlang version is more compact and terse, which is by design - the language prioritises typing speed for live use. However, the C version is easier to read? This isn’t necessarily a problem as the Syntə code would likely be wrapped as a function like [ msg ... ] and the insides wouldn’t need to be examined.
Something makes me feel that the amount of typing required and readability are natural adversaries, so that is a tradeoff to be made. An example being that short variable names are quick to type, while longer ones can convey meaning that tells you what the variable represents.
The other thing to note is the implicit variable that is the signal passed between successive Syntə operations/functions - to the casual eye this is a hidden effect. Which again, is deliberate.
The comparison is something to ponder on at least.
toodle pip
I hope you found that brief diversion as fun as I did, or perhaps learnt something about DSP along the way. As always, I’d be interested to hear any thoughts/comments you have :)